Details

Published: 07 January 2025

The Super Snowflake Sudoku is made of 48 hexagon, 6 partial hexagons with four triangles and 16 partials hexagons with three triangles for a total of 128 triangles.

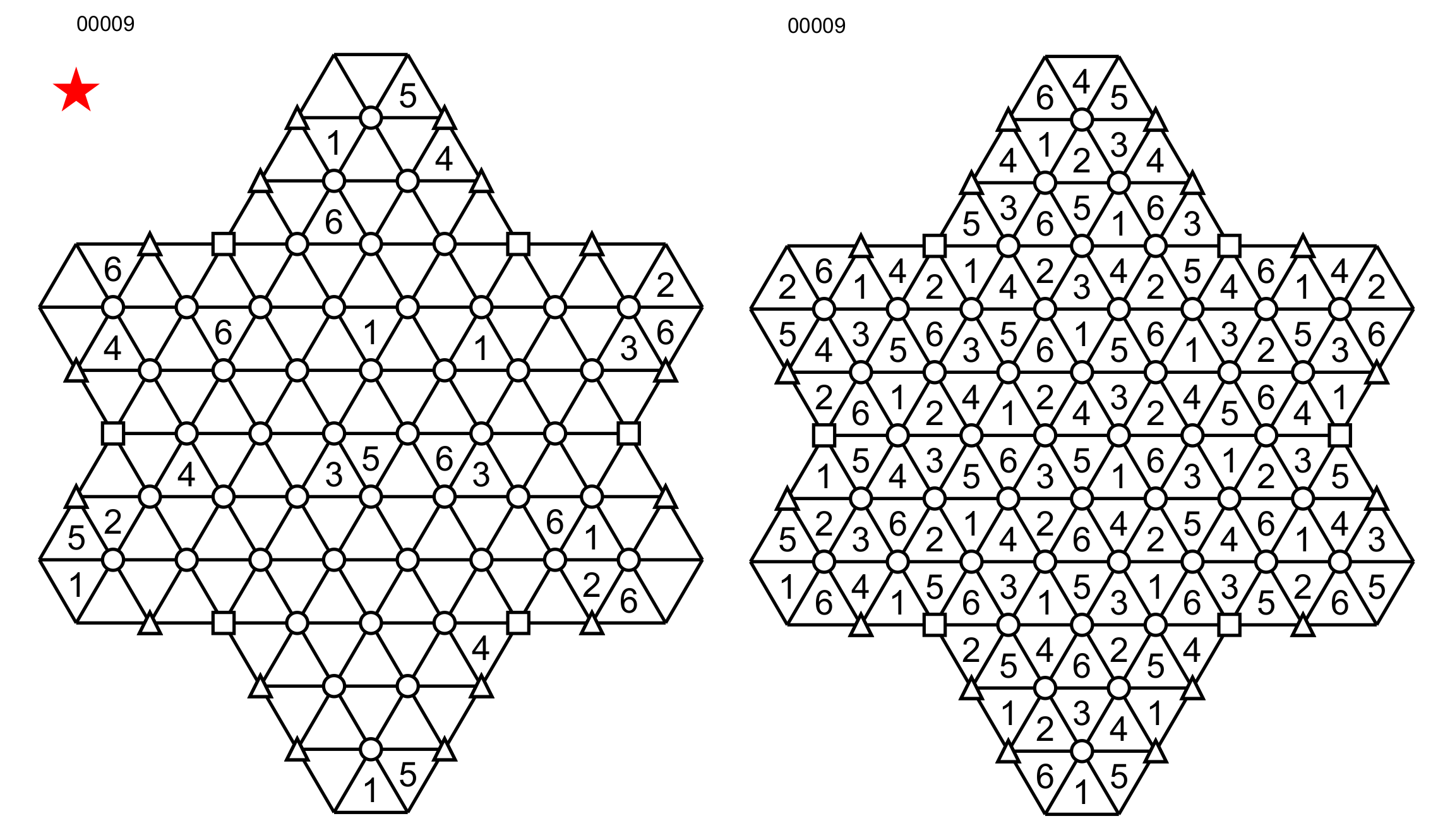
The complete hexagons have a circle at their center (in blue on the picture), and you need to place all the numbers from 1 to 6. 

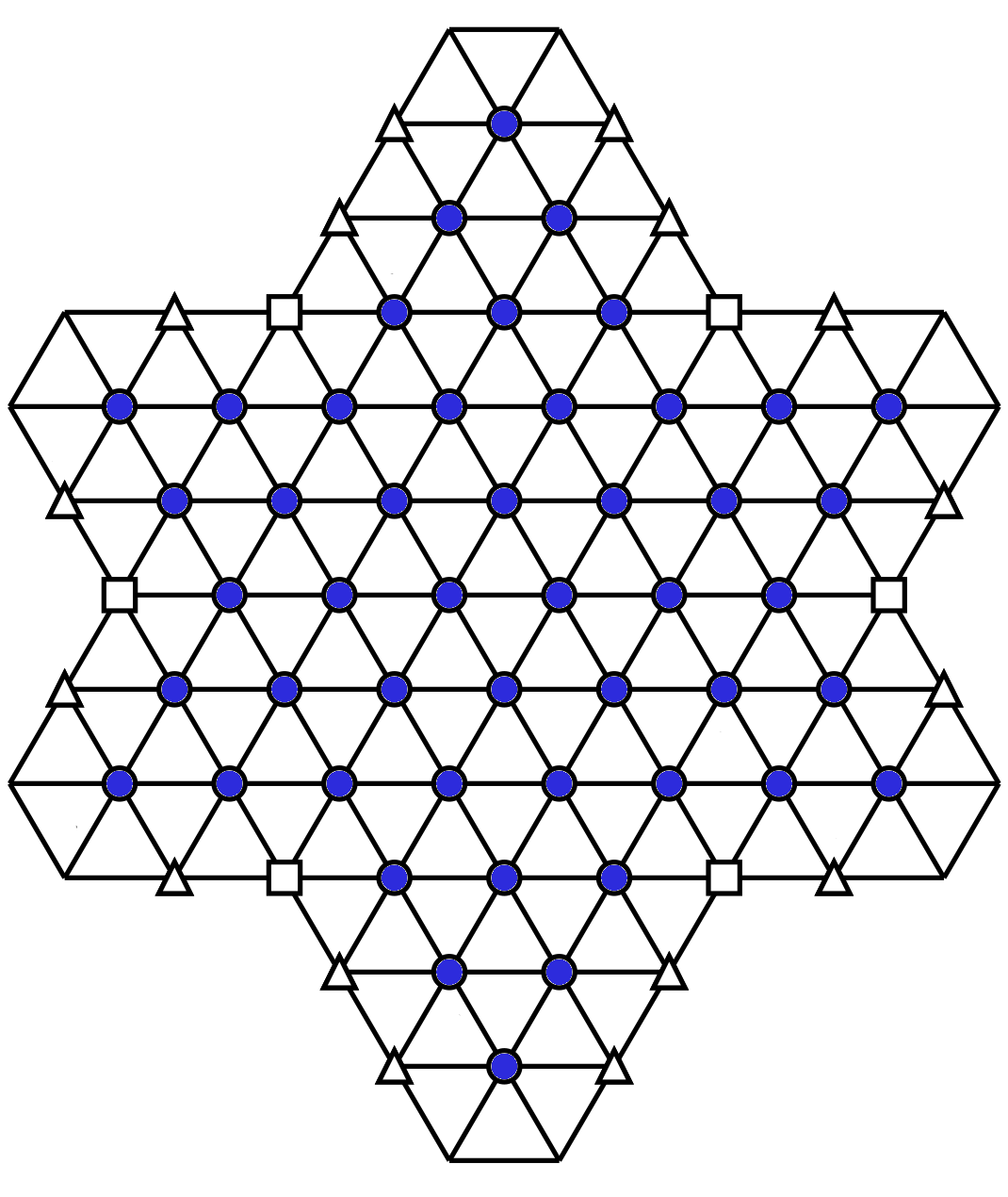
The partial hexagons with 4 triangles have a small square at their center (in red), and you need to place 4 different numbers from 1 to 6 in each triangle.

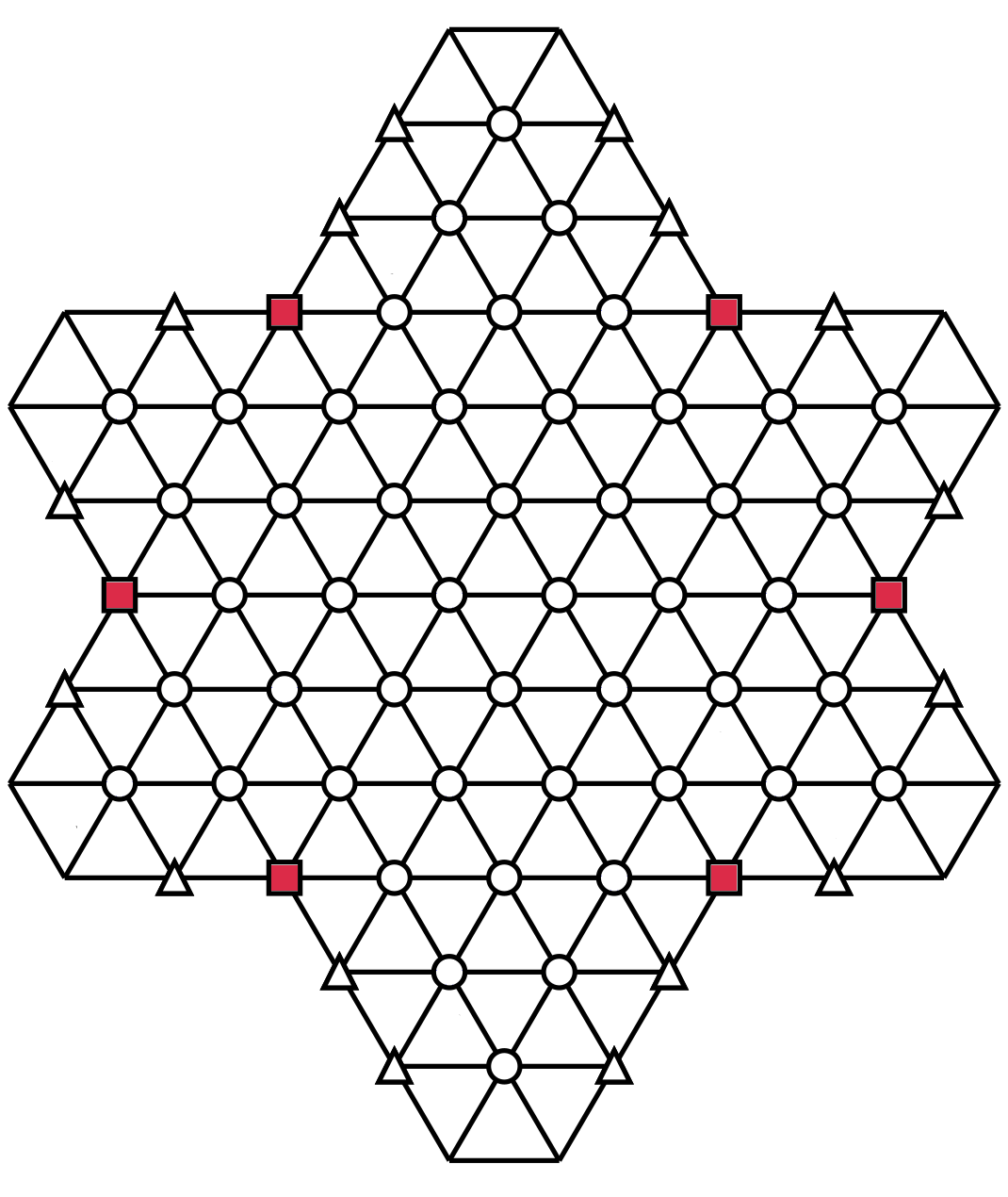
And last but not least: there are 3-triangle partial hexagons with a small triangle at their center (green). Enter 3 different numbers from 1 to 6 around the small triangles.

The addition of partial hexagons with three cells creates more attractive grid shapes.
Note that a triangle in the center of the grid is a member of 3 different hexagons. This geometry makes it possible to apply certain additional resolution rules between them, which I call 3-triangle gaps. If there are two triangles with the same number and these two  triangles point in the same direction, and these two triangles are separated by three triangles, as in the following example.

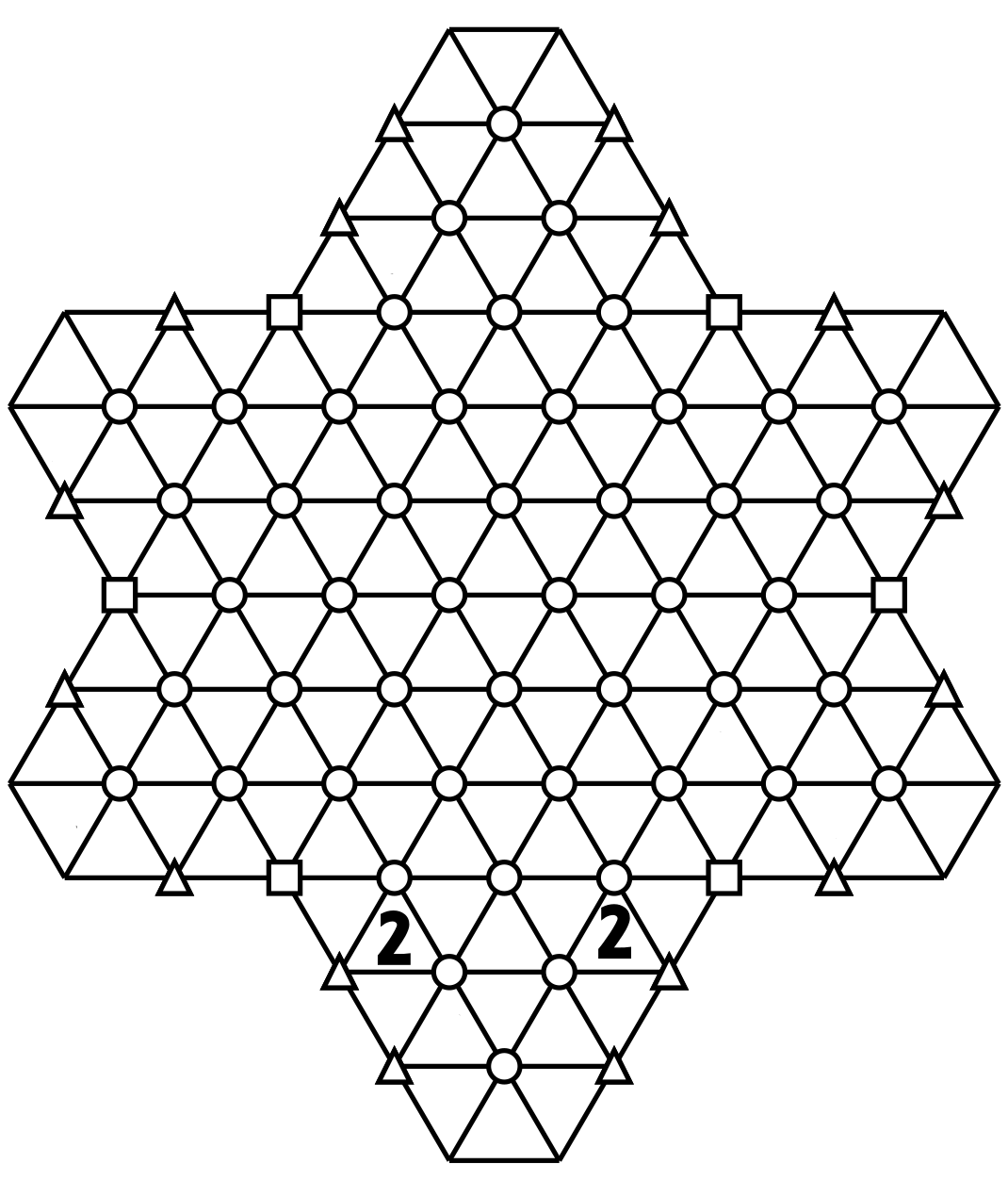
The two triangles point upwards, have the same number and are separated by three cells. We know that both belong to two different hexagons. The first hexagons are outlined in blue.

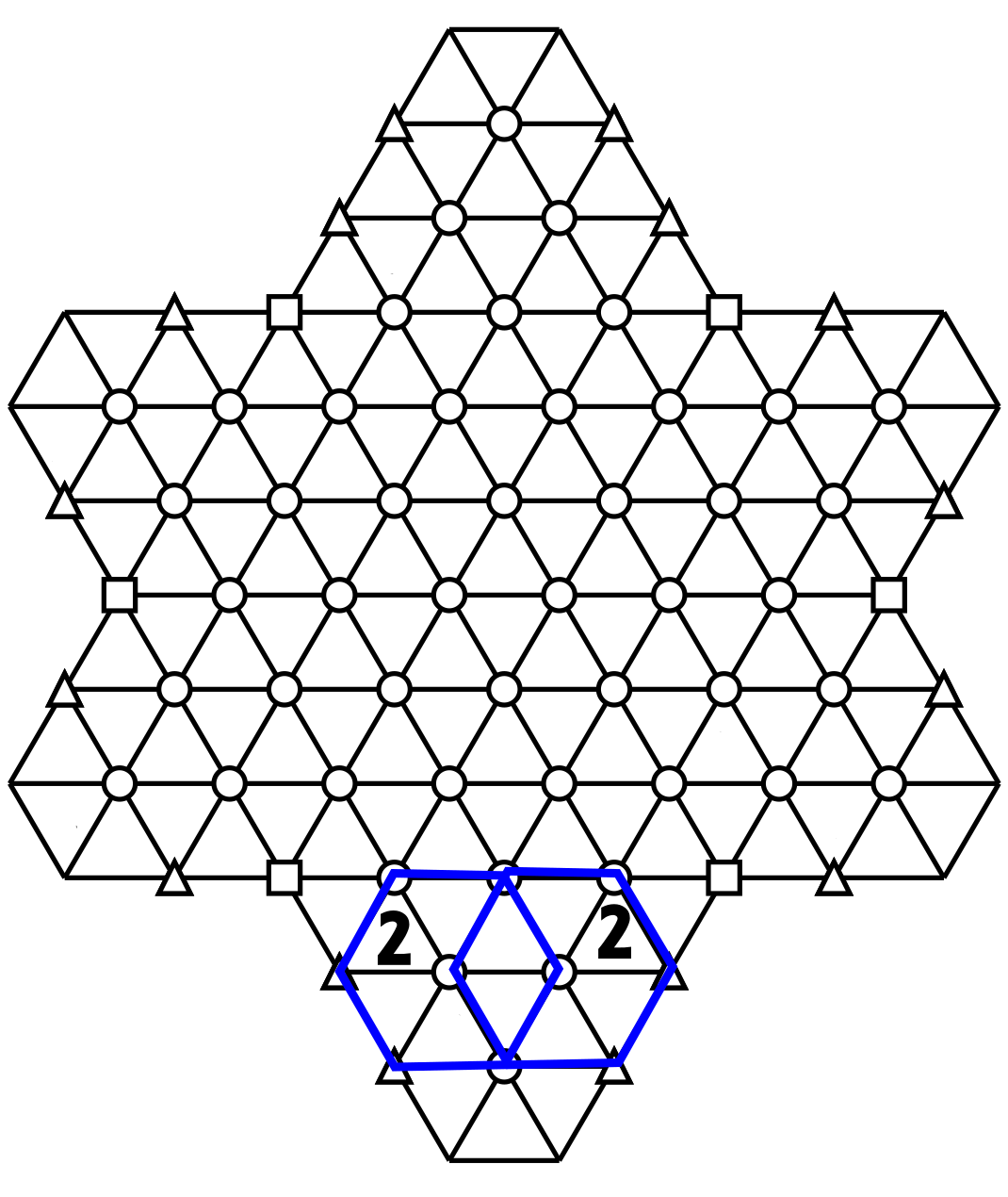
This means that all the triangles in grey) in these first two hexagons will not have a number 2.

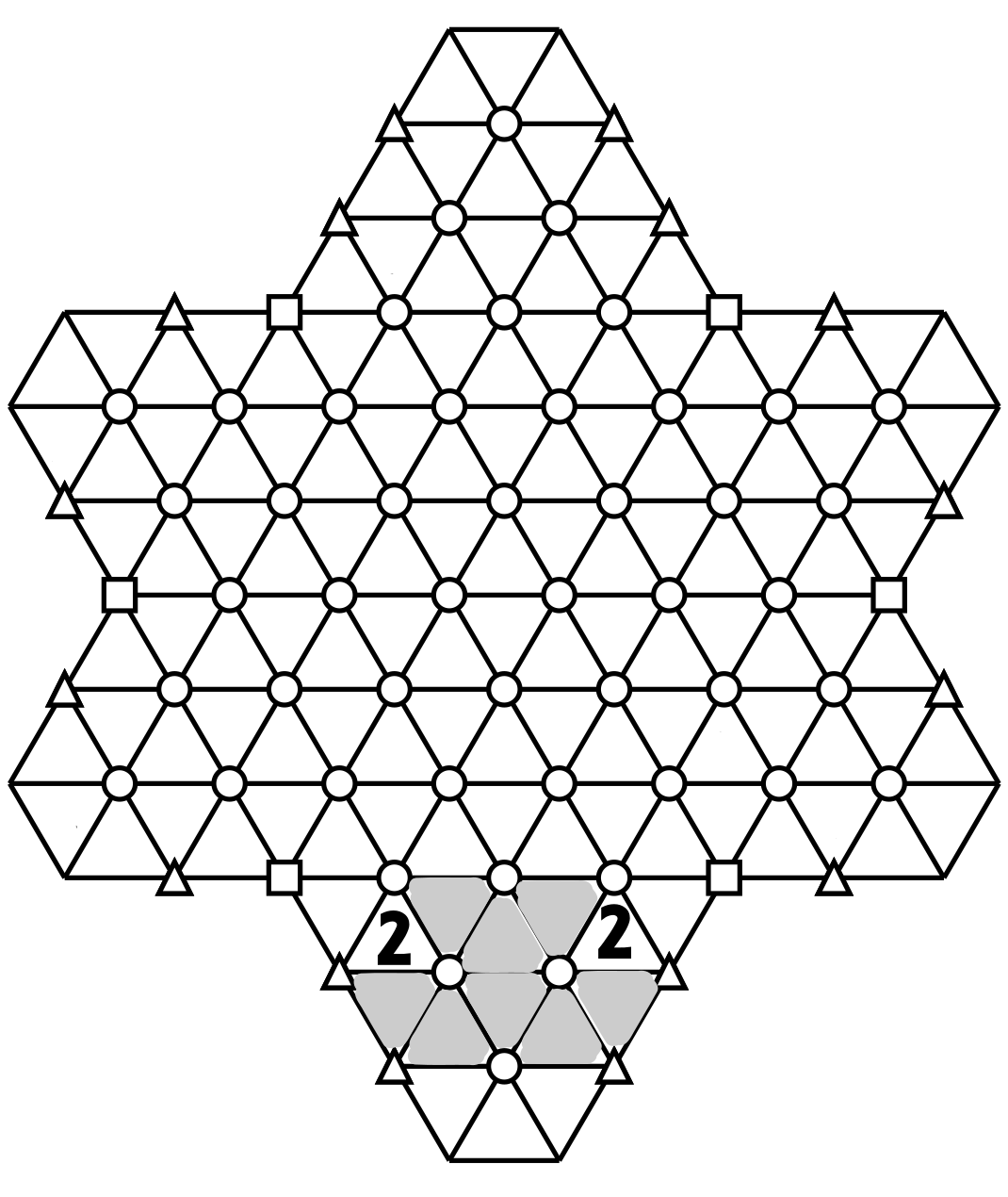
The two other hexagons are delimited by red lines.

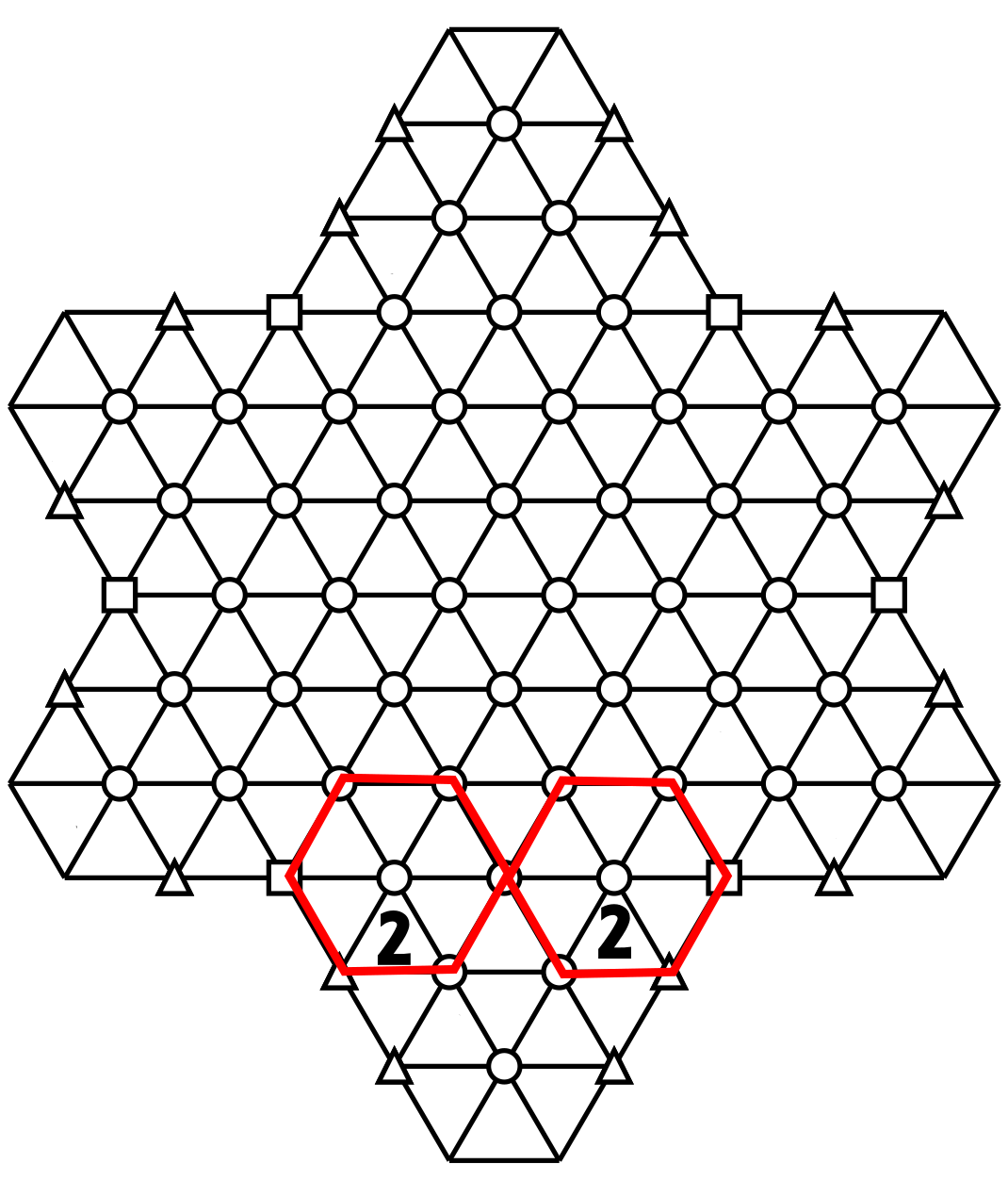
These two hexagons will not have another 2 (except for th two triangles having 2), Then the hexagon between these two triangles having 2, will have a 2 int the center top triangle (in yellow). It will be the only triangle of tis hexagone to have 2.

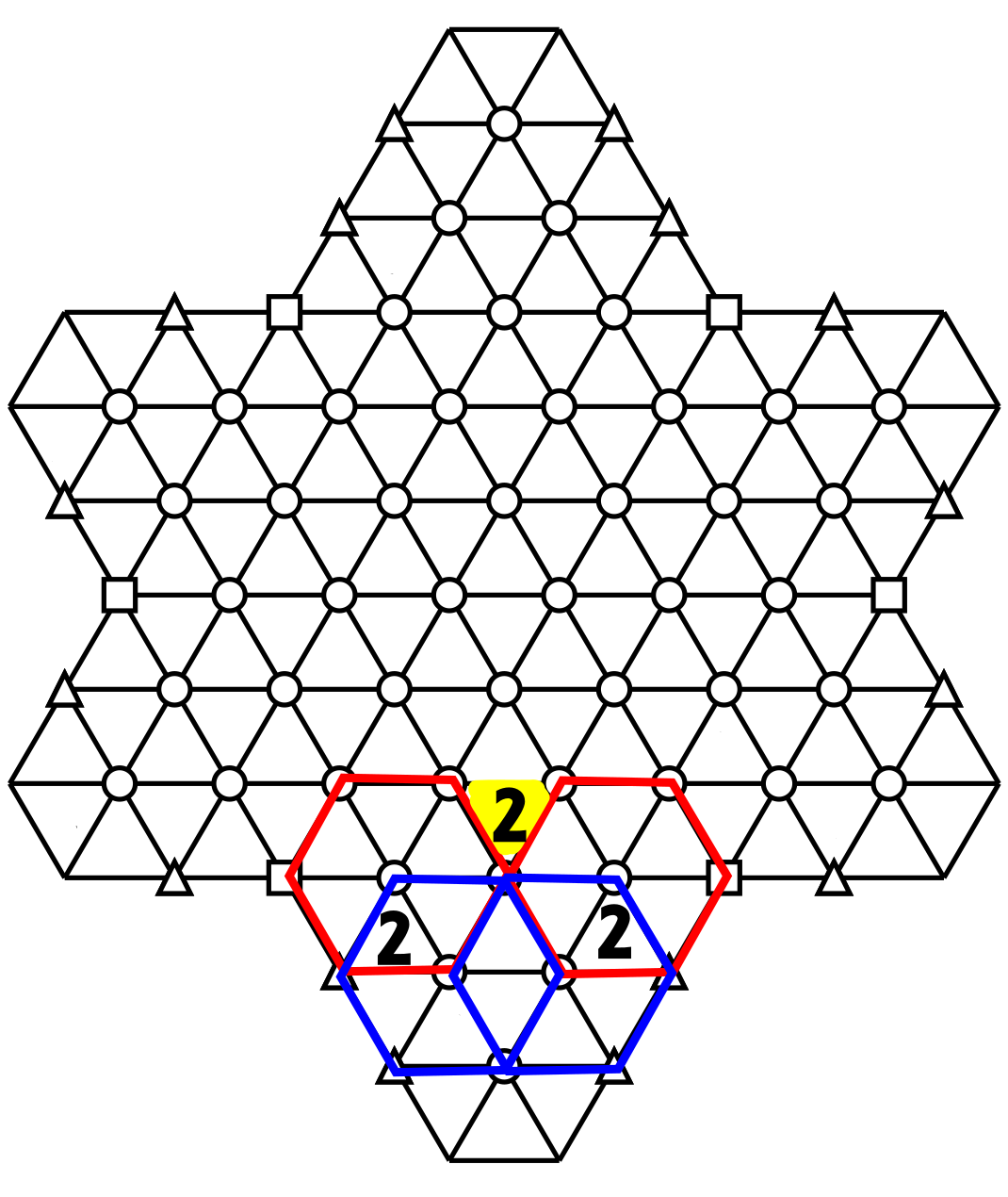
So we can finalize our rule: if two triangles pointing in the same direction have the same number, and these two triangles are separated by 3 triangles, then the upper central triangle of the hexagon between the two triangles will have the same number as those two triangles. 

You will discover more rules as you solve these games.

{ccomment on}

Details

Published: 10 September 2017

GOAL

This technic lets you eliminate one candidate.

Condition

If a cell has n candidates and n neighboring cells pertaining to an another and same region and the neighboring cells have the same candidates than the original cell. If only one another cell (the resulting cell) exists in this region that is not a neighbourg of the original cell and this cell has all the candidates of the original cell plus an extra candidate. Then we could eliminate this extra candidate in this resulting cell.. 

Result

The neighboring cells of the original cell, have all the candidates of the original cell. So its means that if the original cell elects one of its candidates then the neighboring cells will eliminate this candidate and the resulting cell will have this candidate because this is the only other cell having the candidate in the region. At the end this resulting cell will have only the candidate of the original cell. So we could eliminate all the other caniddates in the resulting cell.

Why

This is why I call this technic opposition because ultimely the candidate elected inf the original cell will be in the resulting cell..

EXAMPLE

 

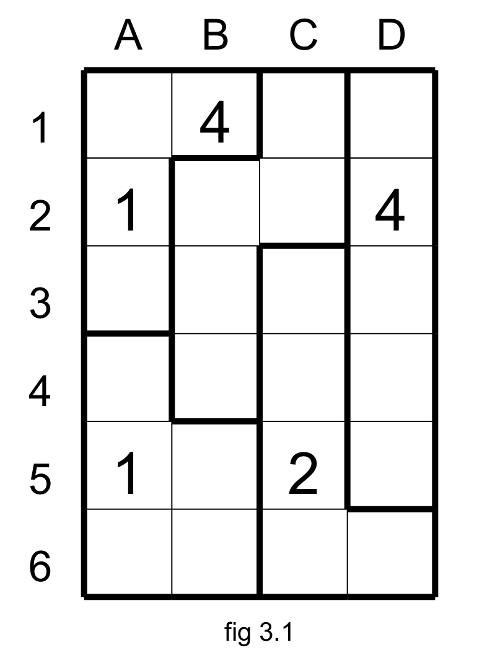
From the Suguru at the figure 3.1 with the basic technics we arrive at this situation (fig 3.2).

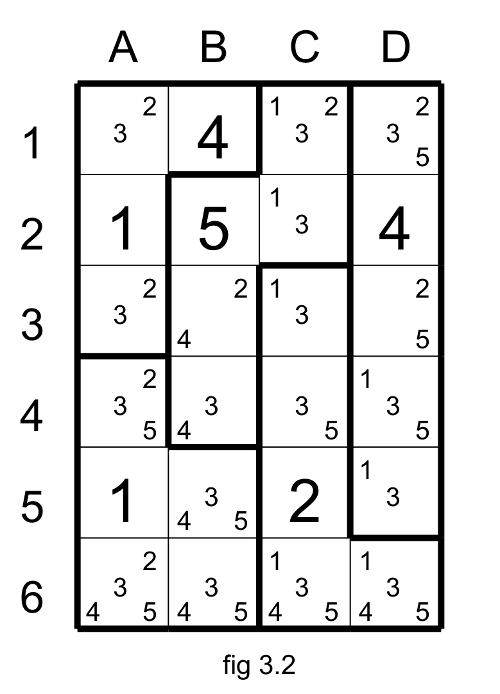
To be able to progress you need to apply the opposition. The original cell c3 has two candidates: 1 and 3 and also two neighboring cells C2 and B4. These two neighboring cells have together the same candidates that the original cell ( 1 and 3  and even one more 4, but we don't care). In this same region it have only one other cell C1 having the same candidates than the original cell (1,3) and also an extra candidate 2.  It is very important to notice that this cell is the only other cell with the neighboring cell C2 and B4 that have the canidates of the original cell. So based on the rule we could eliminate the extra candidate 2 from C1.

 Why 

If the original cell C3 finaly has a 3 then C1 and B4 will eliminate this candidate and C1 will have a 3. And if C3 has 1 then C2 will eliminate the candidate 1 and C1 will have the 1. So in any case C1 will never have the 2. This is why we could eliminate it.  The cells C3 and C1 are in opposition. 

 

With that you could find the solution (fig 3.3).

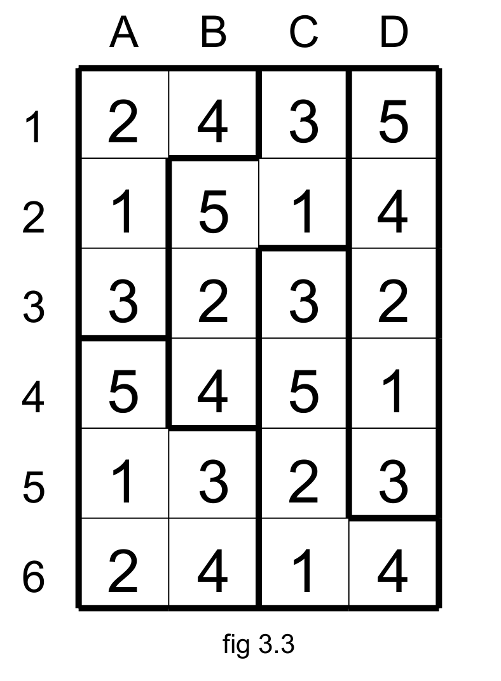
You could try by yourself with this puzzle Suguru Opposition.pdf.

{ccomment on}

Details

Published: 09 September 2017

GOAL

This technic let you eliminate one candidate.

CONDITION

If a cell has n candidates and n neighboring cells pertaining to an another and same region (the region) and the neigboring cells have the same candidates than the original cell plus an another candidate. This another candidat must also appear only once in an aother cell (the another cell) of the region. 

RESULT

Then we can exclude this other candidate in this other cell. Because the extra candidate must appear in the neighboring cells else it will create an illegal situation.

WHY

The extra candidate must appear in the neighboring cells else it will create an illegal situation because the original cell  with n candidats will have n neighbourgs with the same candidats.

EXAMPLE

 

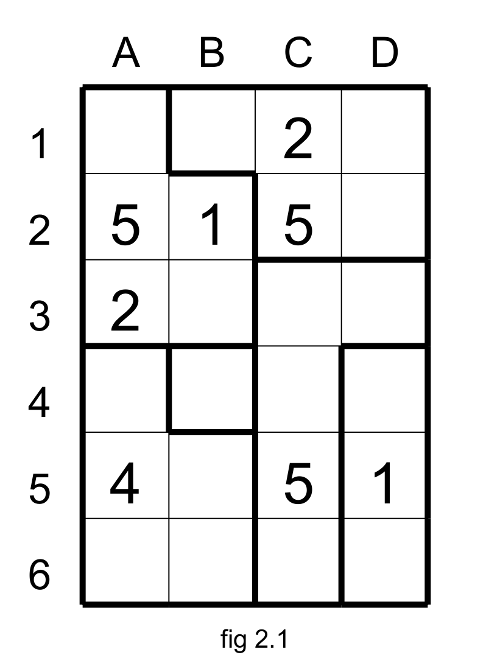
From the Suguru at the figure 2.1 with the basic technics we arrive at this situation (fig 2.2).

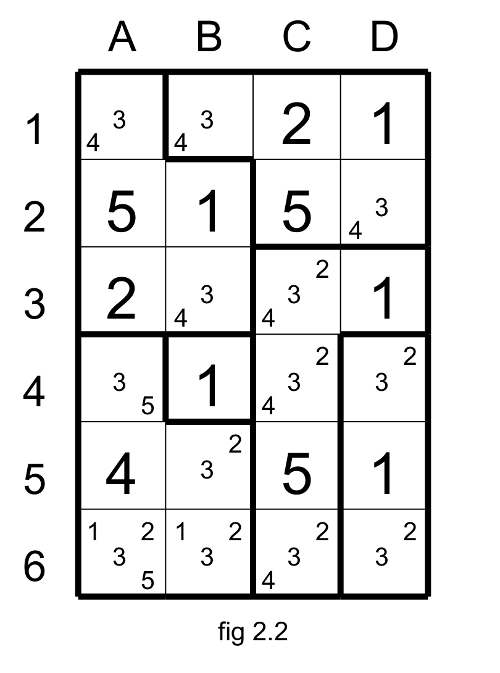
To be able to progress you need to apply the exclusion. The original cell B3 has two candidates: 3 and 4 and also two neighboring cells C3 and C4. These two neighboring cells have together the same candidates than the original cell ( 3 and 4) plus the candidate 2 twice (this is the difference with the technic of the Election, where the extra candidates must be unique in the neighboring cells). And this candidate 2 appears only once in this region (other than the neighboring cells) in C6. So we could eliminate the candidate 2 in C6.

 

Why 

If the cell C6 has 2 then C3 and C4 will have candidates 3 and 4. It will result that B3 will be empty. Note we could also apply this technic with the original cell B5 and its neighboring cells C4 and C6 to eliminate the 4 in C3. 

 

With that you could find the solution (fig 2.3).

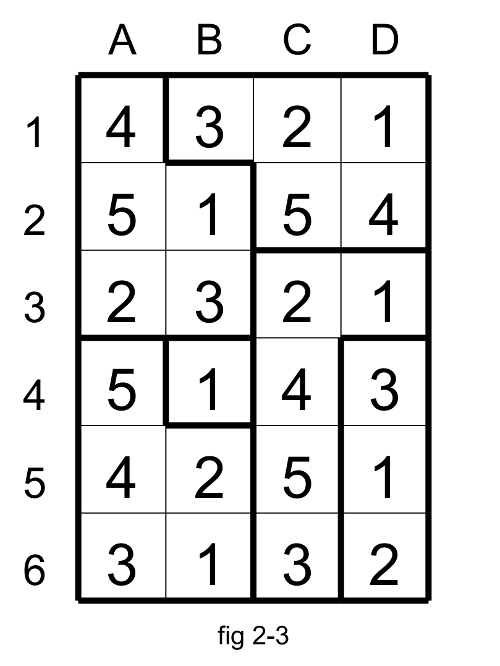
You could try by yourself with this puzzle Suguru exclusion.pdf.

{ccomment on}